728x90
반응형
1. 학습 목표
- 평균, 분산, 표준편차 등의 기초 통계 개념을 이해한다.
- 공분산과 상관계수를 통해 변수 간 관계를 분석한다.
- 선형 회귀에서 통계 개념이 어떻게 활용되는지 이해한다.
2. 데이터의 중심: 평균과 중앙값
(1) 평균 (Mean)
- 모든 값을 더한 뒤 개수로 나눈 값
- 공식:

✅ 예제:

(2) 중앙값 (Median)
- 데이터를 크기순으로 정렬했을 때 중앙에 위치한 값
- 홀수 개 → 가운데 값, 짝수 개 → 가운데 두 수의 평균
✅ 예제:

3. 데이터의 흩어짐: 분산과 표준편차
(1) 분산 (Variance)
- 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 지표
- 공식:
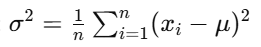

(2) 표준편차 (Standard Deviation)
- 분산의 제곱근 → 단위가 원래 데이터와 같아짐
- 공식:
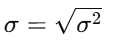
✅ 예제:
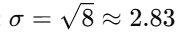
4. 두 변수의 관계: 공분산과 상관계수
(1) 공분산 (Covariance)
- 두 변수의 상관 관계를 측정 (함께 커지거나 작아지는 경향)
- 공식:


(2) 상관계수 (Correlation Coefficient, r)
- 공분산을 각 변수의 표준편차로 나눈 값 → -1 ~ 1 사이
- 공식:

✅ 해석:
- r = 1: 완전 양의 상관
- r = 0: 상관 없음
- r = -1: 완전 음의 상관
5. 통계 개념과 선형 회귀의 연결
- 선형 회귀는 X와 Y의 선형 관계를 찾는 것이므로
- 상관계수 r 이 높으면 선형 회귀 모델이 잘 맞음
- 분산과 표준편차는 오차를 측정하는 데 사용됨 (예: 평균제곱오차)
- 공분산은 회귀계수 계산에 직접적으로 사용됨 (예: 최소제곱법 공식)
6. 연습 문제
- 데이터 X = [2, 4, 6, 8]의 평균과 분산, 표준편차를 구하세요.
- 데이터 X = [1, 3, 5], Y = [2, 6, 10]의 공분산과 상관계수를 구하세요.
- 공분산이 0이면 두 변수는 어떤 관계인가요?
- X의 분산이 클수록 회귀선의 기울기는 어떻게 변할까요?
- 상관계수가 1에 가까울수록 선형 회귀는 어떤 의미를 갖게 될까요?
6. 연습 문제 정답

728x90
반응형
'Study > A.I' 카테고리의 다른 글
| AI 자격증 (AICE) 공부해볼까? AICE 살펴보기 (1) | 2025.06.14 |
|---|---|
| GPT 만들기 완전 정복! 나만의 AI 챗봇을 손쉽게 만드는 방법 (내 GPT) (2) | 2025.05.25 |
| AI스터디를 위한 수학 공부 - [수학] 역행렬(Inverse Matrix) 이해하기 (0) | 2025.05.06 |
| AI스터디를 위한 수학 공부 - [선형회기 사전학습] Day 2: 기초 선형대수 (Linear Algebra) 이해하기 (0) | 2025.02.15 |
| AI스터디를 위한 수학 공부 -[선형회기 사전학습] Day 1: 함수(Function)와 기울기(Slope) 이해하기 (1) | 2025.02.09 |