역시 중,고등학교때 열심히 공부했어야 했다...
공부하려니 역시나 자꾸 이전 단계를 찾아 보게된다...
🔹 역행렬(Inverse Matrix) 이해하기
역행렬은 정사각 행렬(n × n 행렬)에 대해 정의되며, 선형 방정식의 해를 찾는 데 중요한 역할을 합니다.
이를 이해하려면 먼저 행렬 곱셈과 단위 행렬의 개념을 알아야 합니다.
1. 역행렬이란?


여기서 는 단위 행렬(Identity Matrix)로, 대각선 원소가 모두 1이고 나머지는 0인 행렬입니다.
예를 들어, 2×2 단위 행렬은 다음과 같습니다.

즉, 행렬과 그 역행렬을 곱하면 단위 행렬이 된다는 것이 핵심 개념입니다.
2. 역행렬이 존재하는 조건
모든 행렬에 역행렬이 존재하는 것은 아닙니다.
역행렬이 존재하려면 다음 조건을 만족해야 합니다.
✅ 1) 행렬이 정사각 행렬이어야 함
- 즉, n×n 크기의 행렬이어야 한다. (예: 2×2, 3×3 등)
✅ 2) 행렬식(Determinant, det(A))이 0이 아니어야 함
- 행렬식이 0이면 역행렬이 존재하지 않습니다.
- 행렬식(det(A))을 계산하는 방법은 다음과 같습니다.
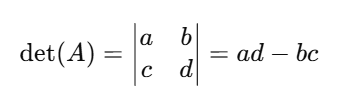
만약 det(A)=0이면 역행렬이 존재하지 않음.
3. 2×2 행렬의 역행렬 구하는 공식
2×2 행렬

의 역행렬은, 행렬식이 0이 아닐 때 다음과 같이 계산됩니다.

단, det(A) = ad - bc ≠ 0 이어야 합니다.
✅ 예제
행렬 A가 다음과 같다고 가정합니다.

1️⃣ 행렬식 계산

2️⃣ 역행렬 계산

✅ 검산 (역행렬이 맞는지 확인)

즉, 단위 행렬이 나오므로 계산이 맞음.
4. 역행렬을 이용한 선형 방정식 풀이
역행렬은 선형 방정식 AX=B를 푸는 데 유용하게 사용됩니다.

위 방정식에서 X 를 구하는 방법:
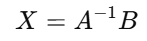
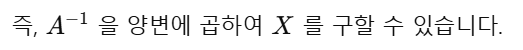

5. 역행렬을 구할 수 없는 경우
만약 행렬식(det(A))이 0이면, 역행렬이 존재하지 않음.
예를 들어,

이 경우,

따라서 역행렬이 존재하지 않음.
이런 행렬을 특이 행렬(Singular Matrix) 이라고 합니다.
6. 정리

🔹 역행렬 연습문제 5개

풀이과정





'Study > A.I' 카테고리의 다른 글
| GPT 만들기 완전 정복! 나만의 AI 챗봇을 손쉽게 만드는 방법 (내 GPT) (2) | 2025.05.25 |
|---|---|
| AI스터디를 위한 수학 공부 - [선형회기 사전학습] Day 3: 통계 기초 (Statistics) 이해하기 (0) | 2025.05.06 |
| AI스터디를 위한 수학 공부 - [선형회기 사전학습] Day 2: 기초 선형대수 (Linear Algebra) 이해하기 (0) | 2025.02.15 |
| AI스터디를 위한 수학 공부 -[선형회기 사전학습] Day 1: 함수(Function)와 기울기(Slope) 이해하기 (1) | 2025.02.09 |
| AI스터디를 위한 수학 공부 - 6일 코스: 선형 회귀 사전 학습 플랜 (1) | 2025.02.09 |